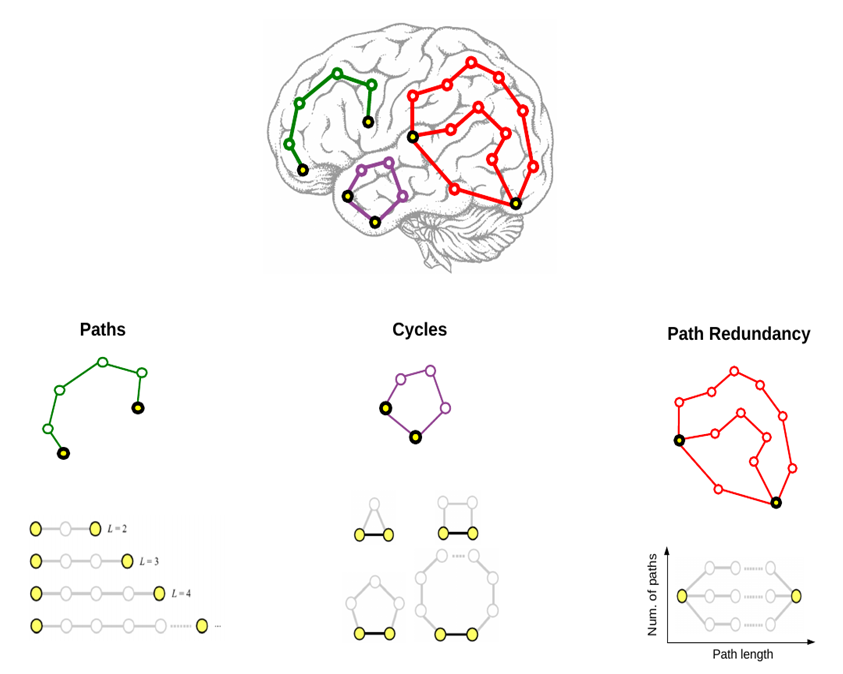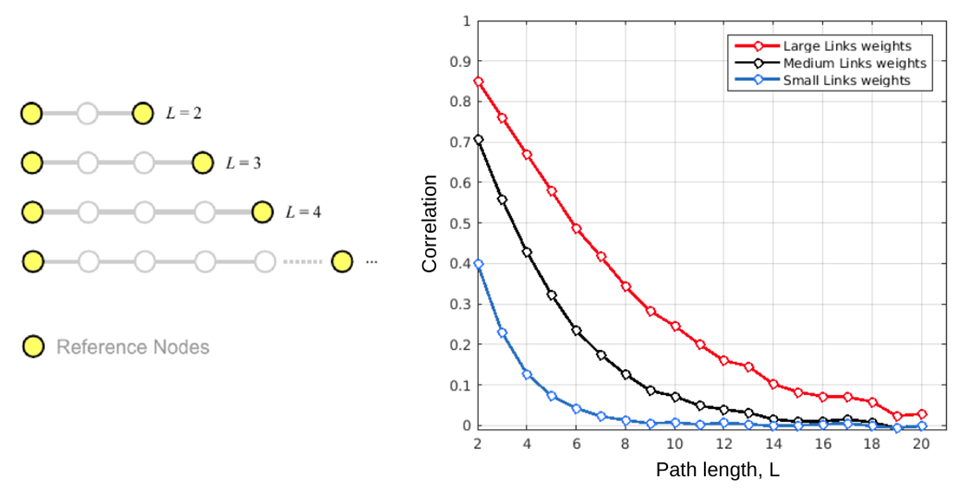
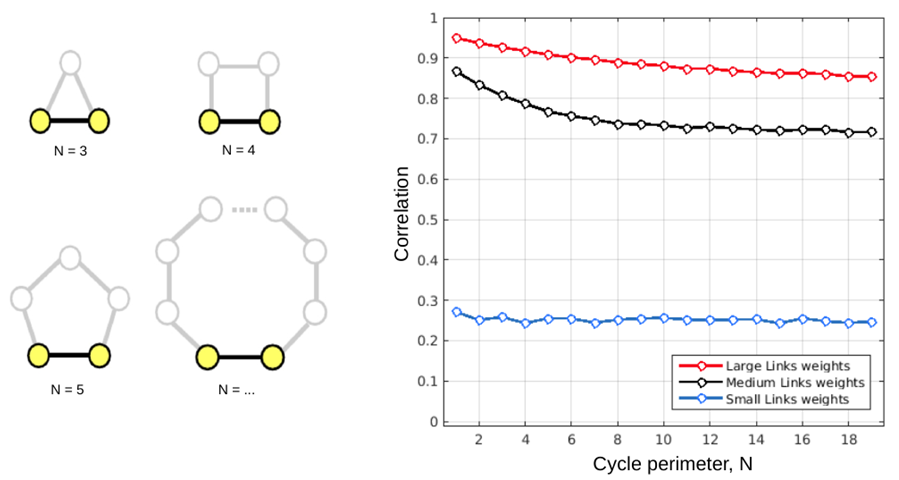
Paths are simple chain structures, i.e. networks of N nodes where N −2 nodes are connected with exactly two other nodes, and the remaining 2 nodes (the two ends of the chain) are connected with only one node. It follows that in a chain of N nodes the total number of links is L = N − 1. In graph theory and applied network science, chains are also referred to as paths (Bang-Jensen and Gutin, 2008), term that I will use interchangeably with chain throughout the current post. In order to quantify the influence that chain structures have on the correlation between the reference nodes (posed at the two extremities of the path), the most relevant topological features to manipulate are on one hand the total length of the chain, L, corresponding to the the number of links separating the two reference nodes, and on the other hand the weights of all L links in the path, each one denoted as w. Nonetheless, trying to systematically evaluate all possible combinations of w for different lengths L is computationally expensive, and its relevance in determining the correlation between the nodes at the two ends is likely small compared to, for example, the mean weight of the whole path. As such, as a first approximation and to reduce the complexity of the model, we chose to assign equal weights w to all L links in the chain, and then exploring how large, medium and small links’ weights influence the correlation between reference nodes for different path lengths. The length of the chain plays a dominant role, as even very strong chains have little effect on the correlation between the reference nodes if they are too long. This pattern of results demonstrates that the size of the correlation between two nodes placed at the extremities of a chain will approximately depend on the inverse of the path length, only modulated by its mean strength.
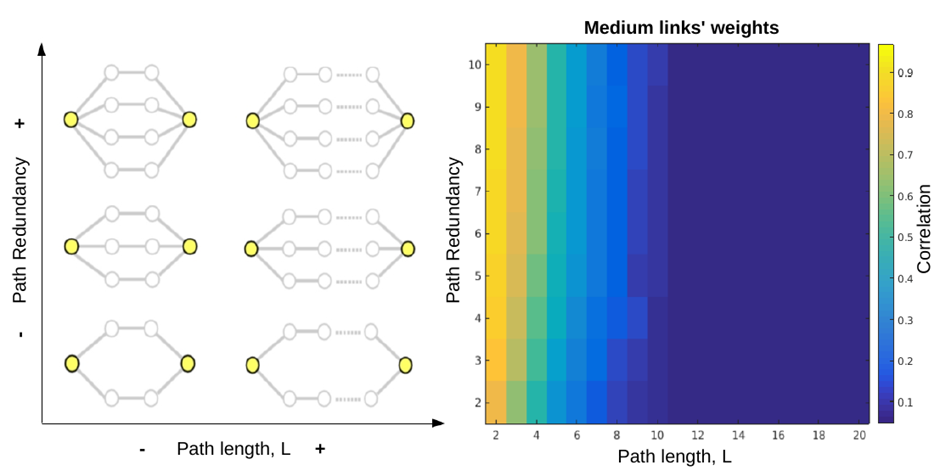
Path Redundancy. Within a simple chain topology, the size of the correlation between the end nodes is mainly determined by the number of links separating them, and modulated by the mean weight of the path. Nonetheless, in networks the number of paths connecting two nodes are usually more than one. To be precise, it is well known that the number of paths of length L between any pair of nodes in a network is given exactly by the powers of the adjacency matrix defining the non-zero links of that network (Biggs 1993; Bang-Jensen and Gutin 2008, see Appendix C.5); this implies that the theoretical total number of paths of any length between each pair of nodes is indeed infinite. Nonetheless, the observations reported in the previous sections (paths, cycles) demonstrate the decay of the influence exerted by long paths on the nodes at its ends and, as such, it is legitimate to restrict our analysis to relatively short paths only. The inherent existence of multiple alternatives paths of different length demonstrate that the connectivity between nodes always tend to display some degree of path redundancy. We thus focused on quantifying the effect of such redundancy on the correlation between a given pair of reference nodes. To this aim, we built chain networks with paths of different length, L, and different mean chain weight, and systematically evaluated how adding paths of the same length (i.e. increasing path redundancy) influenced the correlation between the nodes at the two ends of the path. In accordance to the previous findings, the path length L seems to play a major role in determining the correlation between the reference nodes: if the chain is too long, the correlation between the reference node will be low, independently on the strength of the chain and its redundancy. The mean path weight and path redundancy though modulate the correlation in similar manners, amplifying it when the path is short enough.