In the previous post we analyzed how very simple network architectures could affect the resulting pattern of correlations observed between a given pair of nodes. Nonetheless, it is important to remember that the network models presented above are nothing more than highly schematic examples, useful to develop an intuition of the covariations they can produce and sustain. To some extent, these are amongst the simplest kind of interactions one can expect in weighted, undirected networks having more than two nodes. In fact, real networks are made of interwoven assemblies of those (amongst others) “topological units”, which together form intricate architectures and determine the emergence of complex patterns of interactions. As such, understanding the basic properties of such topological units can be highly informative when it comes to try to understand data obtained from real networks.
According to the results so far, the length of the path connecting two nodes, together with paths redundancy, seem to be two major factors in determining the magnitude of their covariation. Recent work in graph theory (Estrada and Hatano, 2008; Estrada et al., 2012) resulted in determining an accurate measure of the total influence exerted by a given node over another node in the network through all possible paths of all lengths, assigning more relevance to shorter ones; this measure of pairwise communicability relies on an exponential decay of the influence exerted by longer paths, and can be seen as a generalization of the concept of distance.
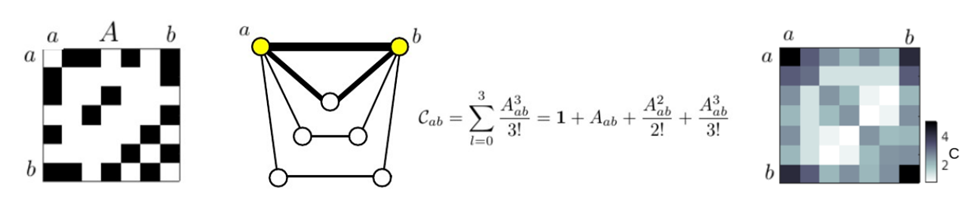
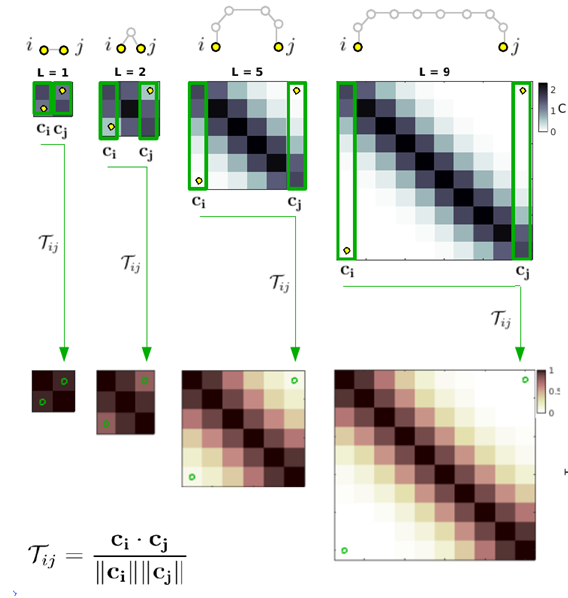
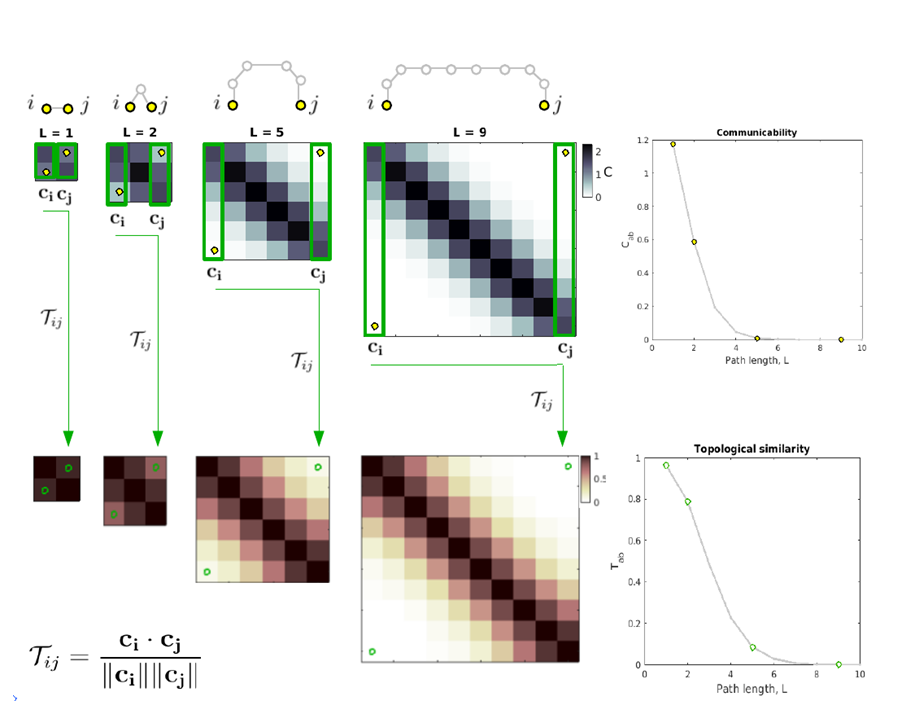
The information summarized by this measure can thus be used to build an estimate of the strength of the covariation that one could expect between two nodes by taking into account the overall similarity of their communicability profiles. To be more specific, if two nodes are connected in similar ways -both with respect to inputs and outputs- with all other nodes in the network, through paths of any lengths (i.e. they have similar communicability profiles), it is legitimate to expect that their chances to display similar behaviors will be high; on the other hand, if the topology of the whole-network communicability between two nodes is very diverse (i.e. they have distinct communicability profiles), their expected coupling will likely be weak.
We proposed a novel measure of the expected baseline correlation between any pair of nodes in the network, based only on their topological similarity. This measure, that we denoted T, compares the similarity of the communicability profiles of different nodes, and as such returns the whole-network topological similarity due to all interweaved paths of any length between every pair of nodes: this measure can thus be reasonably used as a first approximation of the magnitude of the average covariation they will likely exhibit. A quantification of the topological similarity Tij between node i and node j can be obtained computing the the cosine similarity between the entire i-th and j-th column vectors (ci and cj respectively) of the communicability matrix C. It should be noted that the use of the cosine similarity is not the only possible way to measure the topological similarity matrix T, which can in fact be quantified using any other measure of similarity between vectors, such as the Pear. In fact T can be implemented in different ways, depending on the properties of the network under study (binary, weighted, directed, undirected) and on the particular purpose of the analysis. Being based on the communicability matrix C, this particular formalization of the topological similarity T, assumes a very simple diffusive process, and as such differences in this measure are mainly determined by differences in the topological similarity between the two nodes of interest. However, it is important to stress that the original idea behind the concept of topological similarity is in no way bounded to a given formulation of communicability: T can in fact be obtained from any measure quantifying the influence that one node exerts over another node through all paths of all lengths; furthermore, this measure can in principle be applied on any type of system that can be represented as a graph, making the topological similarity T an extremely powerful tool to characterize the whole-system pairwise interactions.
We proposed a novel measure of the expected baseline correlation between any pair of nodes in the network, based only on their topological similarity. This measure, that we denoted T, compares the similarity of the communicability profiles of different nodes, and as such returns the whole-network topological similarity due to all interweaved paths of any length between every pair of nodes: this measure can thus be reasonably used as a first approximation of the magnitude of the average covariation they will likely exhibit. A quantification of the topological similarity Tij between node i and node j can be obtained computing the the cosine similarity between the entire i-th and j-th column vectors (ci and cj respectively) of the communicability matrix C. It should be noted that the use of the cosine similarity is not the only possible way to measure the topological similarity matrix T, which can in fact be quantified using any other measure of similarity between vectors, such as the Pear. In fact T can be implemented in different ways, depending on the properties of the network under study (binary, weighted, directed, undirected) and on the particular purpose of the analysis. Being based on the communicability matrix C, this particular formalization of the topological similarity T, assumes a very simple diffusive process, and as such differences in this measure are mainly determined by differences in the topological similarity between the two nodes of interest. However, it is important to stress that the original idea behind the concept of topological similarity is in no way bounded to a given formulation of communicability: T can in fact be obtained from any measure quantifying the influence that one node exerts over another node through all paths of all lengths; furthermore, this measure can in principle be applied on any type of system that can be represented as a graph, making the topological similarity T an extremely powerful tool to characterize the whole-system pairwise interactions.
Related paper: