For any FC matrix, the algorithm returns an affiliation vector, a vector of length J (being J the number of nodes in the network), where each j-th element of the vector stores the integer labeling the community to which the j-th node has been assigned. Due to the intractability to search the space of all possible partitions, community detection algorithms based on modularity maximization are stochastic, and as such the resulting community partition obtained from a given network may vary from run to run. For this reason, we ran the method M = 100 times, for each FC matrix.
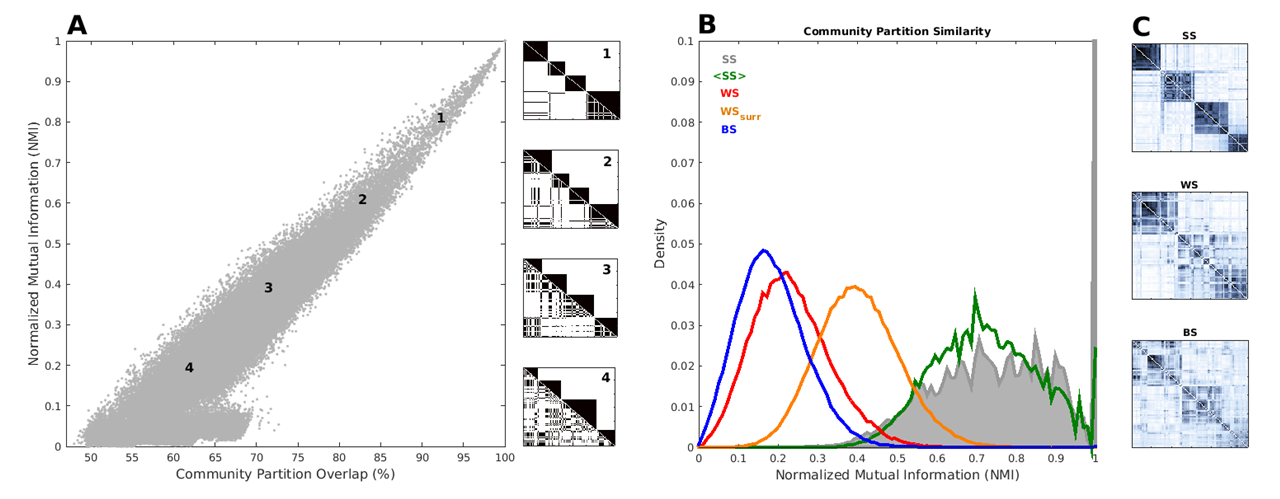
In order to quantify the similarity between any two community partitions A and B, we used the normalized mutual information (NMI), a measure describing how much information one can gain about partition B given that partition A is known, and ranging from 0 (partitions A and B are independent) to 1 (A and B are identical).
Given that NMI can be difficult to interpret at first, we also used another more intuitive (but less sensitive) measure to quantify the degree of similarity between module partitions, namely the percentage of community partitions’ overlap. The communities detection algorithm found only non-overlapping communities, and therefore the minimum value for the communities overlap partition is 0.5.
To have a graphical representation of these variables, NMI and community partitions’ overlap, in panel 1 A we presented some exemplary cases (boxes on the left).