In order to understand synchronization properties of networks embedded into physical space, it is important to take into account the structure of all the interaction between nodes, and these interactions are not only modulated by their spatial arrangement but also by the tightly related time dynamics, which can be summarized as the time delay that a given node needs to influence (or get influenced) by another connected ones. In fact, If we use the brain as an example of a physically embedded network, we immediately realize that the distance between all directly connected regions (or neurons) may vary, implying that the time that a neural signal will need to travel between them will also vary, therefore affecting the synchronization properties and cross-correlations of those neurons and, as a consequence, of the wider network.
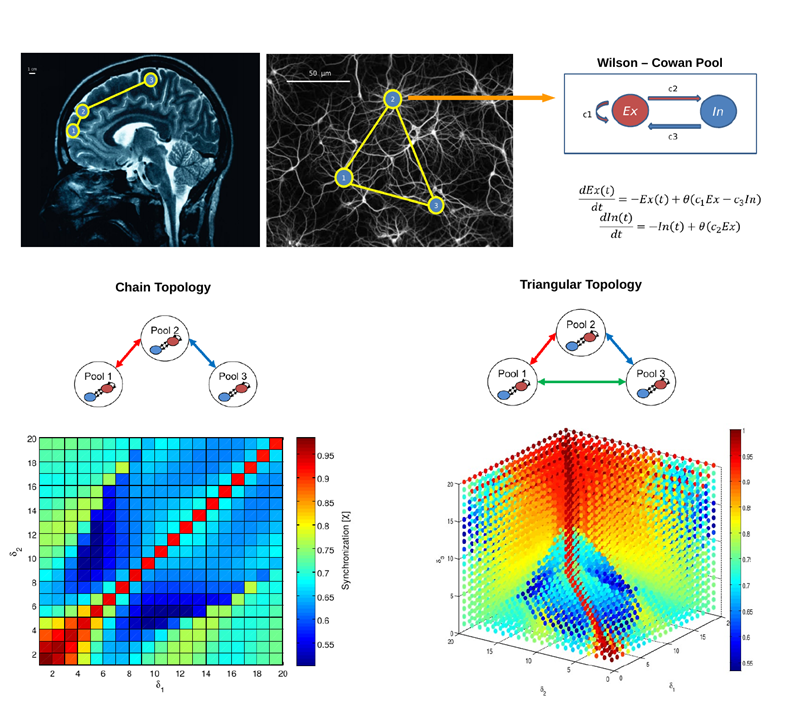
To explore the role of temporal delays in shaping network synchronization properties, we grossly simplified reality by evaluating only two very simple network topologies (chains and triangles) composed of just three coupled nodes modeled as Wilson-Cowan oscillators with fixed connection weights but with varying delays, and then we systematically manipulated the delays between oscillators and calculated the overall network synchronization using the Kuramoto Order Parameter.
Interestingly, we were able to see that apparently the overall synchronization dynamics generated by the two different topologies were highly nonlinear, giving rise to multiple synchronization regions in the delays’ parameter space, highlighting the great influence of the geometry of delays in sculpting network interactions even for the simplest topologies.
Related Papers: